The evolution of an isolated quantum system is unitary. This is simple to probe for small systems consisting of few non-interacting particles. But what happens if the system becomes large and its constituents interact? In general, one will not be able to follow the evolution of the complex many body eigenstates.
Ultra-cold quantum gases are an ideal system to probe these aspects of many body quantum physics and the related quantum fields. Our pet systems are one-dimensional Bose-gases. Interfering two systems allows studying coherence between the two quantum fields and the full distribution functions and correlation functions give detailed insight into the many body states and their non-equilibrium evolution.
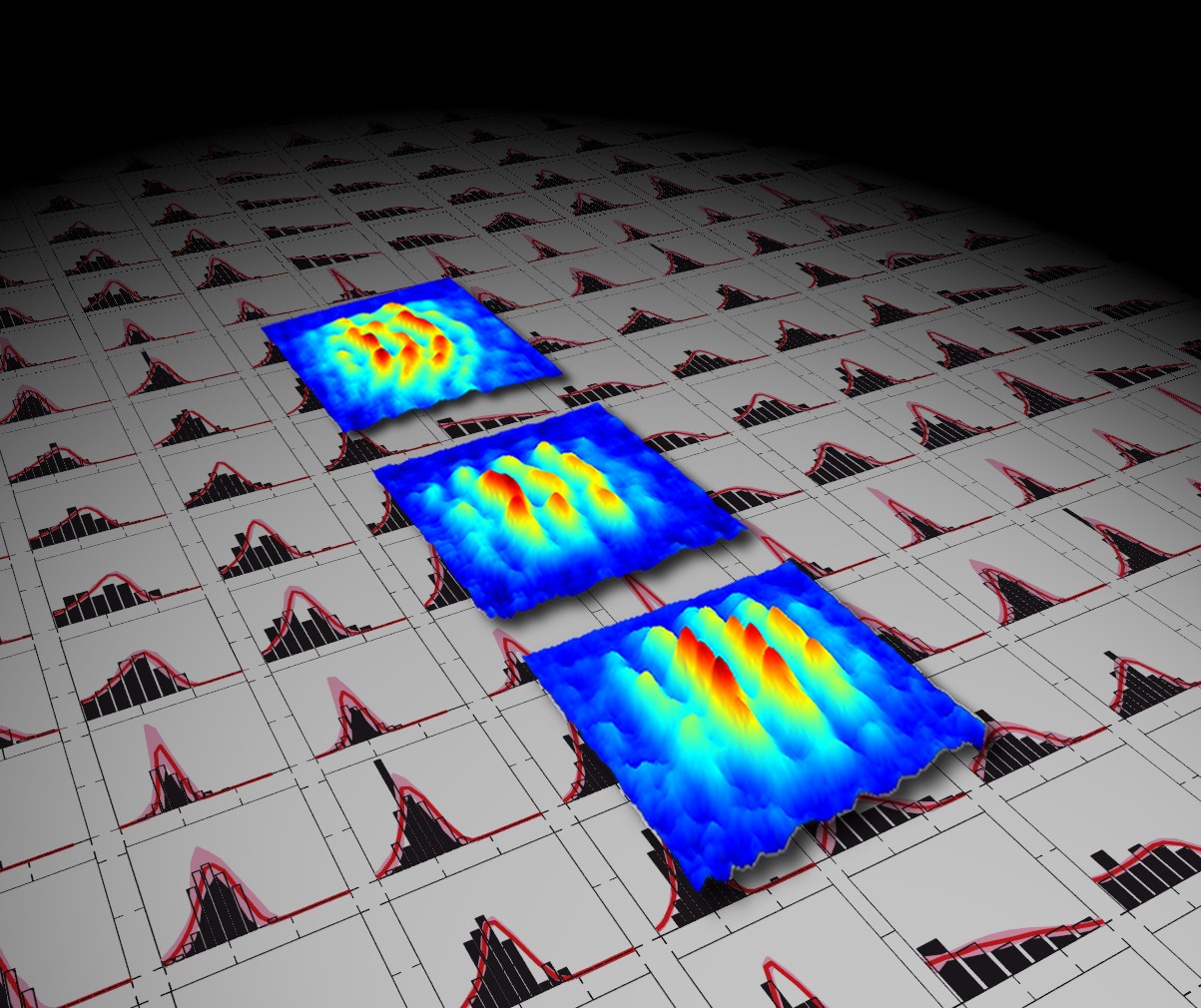
In our experiments, we study how the coherence created between the two isolated one-dimensional quantum gases by coherent splitting slowly degrades by coupling to the many internal degrees of freedom available [1]. We find that a one-dimensional quantum system relaxes to a pre-thermalisatized quasi steady state [2] which emerges through a light cone like spreading of ’de-coherence’ [3]. The pre-thermalized state is described by a generalized Gibbs ensemble [4]. Finally, we investigate the further evolution away from the pre-thermalized state. On one hand, we show that by engineering the Quasiparticles we can create many body quantum revivals [5]. On the other hand, we point to two distinct ways for further relaxation towards a final state that appears indistinguishable from a thermally relaxed state. The system looks like two classically separated objects. This illustrates how classical physics can emerge from unitary evolution of a complex enough quantum system.
We conjecture that our experiments point to a universal way through which relaxation in isolated many body quantum systems proceeds if the low energy dynamics is dominated by scrambling of the eigenmodes of long lived excitations [6].
Work performed in collaboration with the groups of E. Demler (Harvard), Th. Gasenzer und J. Berges (Heidelberg). Supported by the Wittgenstein Prize, the FWF SFB FoQuS, DFG-FWF: SFB ISOQUANT: and the EU: ERC-AdG QuantumRelax
[1] S. Hofferberth et al. Nature, 449, 324 (2007).
[2] M. Gring et al., Science, 337, 1318 (2012); D. Adu Smith et al. NJP, 15, 075011 (2013).
[3] T. Langen et al., Nature Physics, 9, 640–643 (2013).
[4] T. Langen et al., Science 348 207-211 (2015).
[5] B. Rauer et al. Science 360, 307–310 (2018).
[6] T. Langen, T. Gasenzer, J. Schmiedmayer, J. Stat. Mech. 064009 (2016)