A photon-based method for demonstrating the advantage of quantum over classical machines can handle photon loss, facilitating experiments.
A race is on to build a quantum computer that solves difficult problems much faster than a classical computer—a milestone dubbed quantum supremacy [1]. Runners in this race, however, are faced with a hazy finish line, which can move closer as quantum machines and algorithms improve or further away as their classical counterparts catch up. An experiment led by Jian-Wei Pan of the University of Science and Technology in China [2] nudges the racers forward for now. Inspired by a theoretical proposal, the researchers confirmed that a promising method for demonstrating quantum supremacy, known as boson sampling with photons (Fig. 1), produces useful output even as photons leak from the system. This means that researchers don’t have to “toss away” the output of a sampling experiment when photons are lost, as was previously assumed [3], allowing for faster computations and bringing a demonstration of quantum supremacy closer to reality.
When will we have a useful quantum computer? To make the answer concrete, consider the most famous quantum-computing algorithm—factoring large prime numbers [4]. This task will likely require millions, and possibly billions, of quantum bits (qubits) and an even larger number of the devices, or “gates,” that manipulate the qubits. Since today’s most advanced quantum computers have around 50 qubits, a quantum computer that could quickly factor large numbers is probably a long way off.
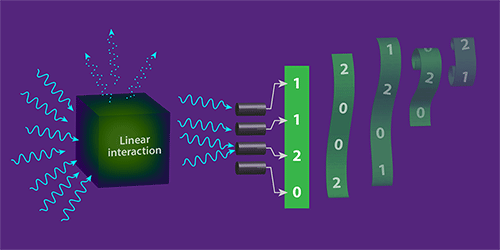
Figure 1: Boson sampling is a task that’s much more efficiently done on a quantum computer than a classical one. A boson-sampling device with photons takes an input of photons, allows them to interact for a period of time, and then measures their positions (th... Show more
But a question with a more encouraging answer is this: what's the bare minimum of quantum resources required to demonstrate the power of quantum computing? Researchers have approached this question by using so-called quantum sampling problems. These tasks generate random outputs, or “samples,” with a particular probability distribution. While this distribution isn’t necessarily useful, producing the samples is relatively simple on a quantum machine. And, crucially, simulating the same distribution of random outputs with purely classical computing resources is proven (under some plausible conjectures) to be exponentially slower.
Boson sampling [5], the subject of the Pan team’s work, is one of two main quantum-sampling approaches [6]. It involves three steps: prepare N single bosons (usually photons), create a linear interaction among them, and detect the locations of the bosons after the interaction (Fig. 1). The boson positions measured after each experiment provide a random sample, and the statistical distribution of multiple samples depends on the nature of the interactions. The challenge for a classical simulation would be to generate the same distribution as the quantum machine assuming the same interactions between the bosons. Estimates suggest that a boson-sampling device would need only about 100 photons before it could produce a random output that would be impractical for a classical device to simulate [7].
The current estimate, however, depends on a few factors. One is the choice of algorithm for generating the sample on a classical computer; such algorithms are continually being improved, which makes classical machines tougher to beat. Another factor is that experimentalists are getting better at eliminating the imperfections in a quantum machine that slow it down. Finally, the proof that the boson-sampling problem is exponentially hard for a classical computer can be adapted to describe imperfect quantum machines. These modified proofs make demonstrations of quantum supremacy involving many bosons more practical.
Pan and colleagues’ experiments are inspired by just such a modification [8]. In 2016, Scott Aaronson and Daniel Brod showed that a boson sampling distribution with a fixed number of lost photons could still outperform classical devices. Pan and colleagues’ work is a small-scale proof-of-principle demonstration that boson sampling with this kind of loss can still be done successfully on a quantum device. As a photon source, the researchers used a semiconductor quantum dot embedded in a multilayered cavity. The dot behaves like an artificial atom, emitting single photons when excited by a laser; the cavity improves the rate and quality of the single photons produced. The photons are then sent through an array of 16 trapezoidal optical elements that are bonded together. This array creates an effective network of pathways for the photons, which experience a linear interaction with one another at various points. Finally, single-photon detectors at the exit ports of the network determine the positions of the arriving photons (the sample). The network is expressly designed to prevent practically any photon loss, with the majority of lost photons coming from inefficiencies in the photon source and detectors.
Previous boson sampling experiments like this one avoided the issue of loss by postprocessing the data and rejecting samples that had too few photons [3]. Pan’s group, by contrast, analyzes samples made up of fewer photons than had been sent by the source. By adjusting the way the photons are fed into the optical network, the researchers could inject from 1 to 7 single photons. They then ensured the sampling task was working correctly by assessing the distribution of detected photons with statistical tests, adjusting these tests to apply to cases where fewer photons arrive at the detector than left the source. The researchers showed that many of these “lost photon” samples are useful, leading to a dramatic improvement in the data acquisition rate. For example, allowing for 2 out of 7 photons lost, the team can collect samples 1000 times per second—at least 10,000 times faster than if they had only collected samples with zero photons lost.
As it stands, this experiment is still far from producing an output that is intractable for a classical computer to generate. More photons and lower loss rates are required to reach that goal. In addition, Aaronson and Brod’s proof rests on the assumption that a fixed number of photons are lost in an experiment, a condition Pan’s team was able to meet in their small-scale setup. But doing so with more photons may be tough, as fixing the fraction, rather than the number, of photons lost is experimentally more realistic. The real message of this experiment is to not fear optical loss in boson sampling. With further theoretical and experimental work, researchers will have a more complete picture of boson sampling with loss, allowing them to forge new paths to a demonstration of quantum supremacy.
This research is published in Physical Review Letters.
References
- The coining of the term “quantum supremacy” is attributed to J. Preskill in arXiv:1203.5813.
- H. Wang et al., “Toward Scalable Boson Sampling with Photon Loss,” Phys. Rev. Lett. 120, 230502 (2018).
- For a list of previous experiments see the section “Experimental Implementations of BosonSampling” in A. P. Lund, M. J. Bremner, and T. C. Ralph, “Quantum sampling problems, BosonSampling and Quantum Supremacy,” npj Quant. Inf. 3, 15 (2017).
- P. W. Shor, “Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer,” SIAM J. Comput. 26, 1484 (1997).
- S. Aaronson and A. Arkhipov, “The Computational Complexity of Linear Optics,” Theor. Comput. 9, 143 (2013).
- A. W. Harrow and A. Montanaro, “Quantum Computational Supremacy,” Nature 549, 203 (2017).
- A. Neville, C. Sparrow, R. Clifford, E. Johnston, P. M. Birchall, A. Montanaro, and A. Laing, “Classical Boson Sampling Algorithms with Superior Performance to Near-Term Experiments,” Nat. Phys. 13, 1153 (2017).
- S. Aaronson and D. J. Brod, “BosonSampling with Lost Photons,” Phys. Rev. A 93, 012335 (2016).